
Jaring-jaring adalah bentuk bangun ruang setelah dilakukan pembelahan. Sekumpulan bangun datar dapat disusun menciptakan bangun ruang. Dalam mempelajari jaring jaring balok, penting juga untuk memahami rumus dari jaring-jaring balok.
Kali ini SemutAspal membahas tuntas jaring-jaring balok.
Pengertian
Pengertian balok adalah bangun ruang yang disusun oleh tiga pasang persegi atau persegi panjang, dengan minimal satu pasang memiliki ukuran yang berbeda.
Sedangkan jaring-jaring balok adalah sisi balok selepas dipotong mengikuti alur rusuknya. Ciri dan karakteristik jaring-jaring balok bisa dilihat jika itu ditekuk akan menciptakan bangun balok.
Jaring jaring balok punya bermacam variasi dan model, karena sisinya terdiri atas persegi panjang dan persegi. Dengan memotong balok pada rusuknya, dapat dihasilkan jaring jaring balok.
Ciri Ciri Balok
Sebelum melangkah lebih jauh, perlu diketahui bahwa balok memiliki ciri khusus yang membedakan balok dengan jenis bangun lain. Balok adalah jenis bangun ruang yang memiliki beberapa hal berikut:
- Terdapat 12 rusuk
- Memiliki 8 sudut
- Terdapat 6 sisi dengan tiga pasang sisi sama besar
- Memiliki 4 diagonal ruang
- Mempunyai 12 diagonal bidang
- Sudutnya pasti siku-siku
Perbedaan Kubus dan Balok
Berikut perbedaan jaring-jaring kubus dan balok, yang antara lain:
- Bentuk sisi keduanya berbeda. Pada balok, cara memotong yang sama dapat berbeda bentuk jika diawali dari sisi yang lain.
- Jaring jaring kubus memiliki sisi berbentuk persegi, sementara jaring jaring balok terdapat persegi panjang dan persegi.
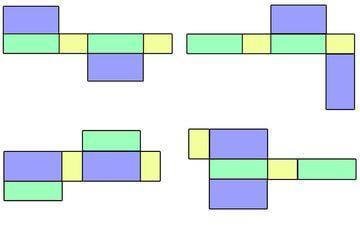
Sifat-Sifat dan Bagian
Berikut beberapa sifat khusus pada balok:
- Ada 6 sisi yang terbentuk dari bangun datar persegi panjang atau persegi
- Terdapat 3 pasang sisi
- Paling tidak terdapat sepasang sisi persegi
- Terdapat 12 rusuk
- Terdapat 4 diagonal sisi
- Diagonal sisi yang sejajar ukurannya sama
- Terdapat 4 diagonal ruang dengan ukuran dan bentuk yang sama
- Bidang diagonal balok memiliki bentuk persegi panjang
- Rusuk sejajar panjangnya sama
Praktik Jaring Jaring Balok
Cara untuk membuat jaring jaring balok dilakukan dengan langkah-langkah berikut ini.
- Siapkan kardus atau karton berbentuk balok.
- Gunting rusuk balok pada titik tertentu untuk membagi balok.
- Biarkan satu sisi samping dan satu sisi bawah.
- Baringkan balok yang digunting pada tempat datar.
- Jaring jaring balok terlihat.
Unsur-Unsur
Setelah praktik menggunting kardus jadi jaring jaring balok, dapat diketahui bahwa jaring-jaring ini:
- Terdapat enam sisi berbentuk persegi panjang.
- Ada tiga pasang persegi panjang berukuran sama.
- Bangun ABCD seukuran dengan EFGH.
- Bangun EHDA seukuran dengan BCGF.
- Bangun ABFE seukuran dengan DCGH.
- Diagonal sisi adalah garis antara dua sudut berhadapan pada sisi balok. Total, balok memiliki 12 diagonal bidang.
- Rusuk adalah perpotongan dua sisi balok yang seperti kerangka penyusun balok. Total, balok mempunyai 12 rusuk.
- Sudut adalah perpotongan dua atau tiga rusuk. Total, balok mempunyai 8 titik sudut.

Contoh Soal Balok
Untuk memudahkanmu memahami gambar sebelumnya, berikut disajikan soal soal terkait balok.
1. Volume dan Luas Permukaan Balok
Hitunglah luas permukaan serta volume balok dengan panjang 6 cm, lebar 3 cm, dan tinggi 4 cm!
Jawab:
Panjang = 6 cm
Lebar = 3 cm
Tinggi = 4 cm
Ditanya:
Luas permukaan (Lp)
Volume (V)
Pembahasan:
V = p x l x t
V = (6 x 3 x 4) x 1 cm³
V = 72 cm³
Lp = 2 x ((p x l) + (p x t) + (l x t))
Lp = 2 × ((6 × 3) + (6 × 4) + (3 × 4)) x 1 cm²
Lp = 2 × (18 + 24 + 12) x 1 cm²
Lp = 2 × 54 x 1 cm²
Lp = 108 cm²
Jadi, volume balok ini 72 cm³ dan luas permukaannya 108 cm².
2. Tinggi Balok
Terdapat sebuah balok dengan volume 7120 cm³. Bila panjang balok tersebut adalah 10 cm dan lebarnya 8 cm. Dapatkan tinggi balok itu!
Jawab:
Volume = 720 cm³
Panjang = 10 cm
Lebar = 8 cm
Ditanya: Tinggi balok
Pembahasan:
t = V ÷ p ÷ l
t = (720 ÷ 10 ÷ 8) x 1 cm
t = 9 cm
Jadi, tinggi balok tersebut adalah 9 cm.
3. Luas Permukaan Balok
Mari hitung luas permukaan balok dengan dimensi berikut: panjang 20 cm, tinggi 10 cm, dan lebar 14 cm. Bagaimana kita bisa menghitung luas permukaan balok ini?
Jawab:
Panjang = 20 cm
Lebar = 14 cm
Tinggi = 10 cm
Pembahasan:
L = 2 (pl + lt + pt)
L = 2 ((20×14) + (14×10) + (20x 10)) × 1 cm²
L = 2 (280 + 140 + 200) × 1 cm²
L = 2 × 620 × 1 cm²
L = 1240 cm²
Jadi, luas permukaannya 1240 cm².
4. Tinggi dan Luas Permukaan
Terdapat balok dengan volume 480 cm³. Panjangnya 10 cm lalu lebarnya 8 cm, berapakah tinggi dan luas permukaan bangun ini?
Jawab:
Volume = 480 cm³
Panjang = 10 cm
Lebar = 8 cm
Pembahasan:
Kamu bisa pakai rumus volume balok untuk mendapatkan tinggi balok ini.
V = p x l x t
480 = (10 x 8 x t) x 1 cm
480 = (80 x t) x 1 cm
t = (480 : 80) x 1 cm
t = 6 cm
Didapatkan tinggi balok ini 6 cm. Luas permukaan balok bisa didapatkan dengan cara berikut ini.
Luas Permukaan
= 2 x ((p x l) + (p x t) + (l x t))
= 2 x ((10 x 8) + (10 x 6) + (8 x 6)) x 1 cm²
= 2 x (80 + 60 + 48) x 1 cm²
= 2 x 188 x 1 cm²
= 376 cm²
Ditemukan luas permukaan balok ini 376 cm².
5. Lebar Balok
Suatu balok dengan volume 336 cm³ memiliki panjang 8 cm serta tinggi 6 cm. Berapa lebar balok ini?
Jawab:
Volume = 336 cm³
Panjang = 8 cm
Tinggi = 6 cm
Ditanya: Lebar balok
Penghitungan:
l = V ÷ p ÷ t
l = (336 ÷ 8 ÷ 6) x 1 cm
l = 7 cm
Lebar balok ini adalah 7 cm.
6. Hitung Luas Permukaan
Hitunglah luas permukaan balok dengan mengambil ukuran lebar sebesar 8 cm, panjang sebesar 9 cm, dan tinggi sebesar 7 cm.
Jawab:
Panjang = 9 cm
Lebar = 8 cm
Tinggi = 7 cm
Ditanyakan: Luas permukaan
Pembahasan:
Lp = 2 x ((p x l) + (p x t) + (l x t))
Lp = 2 x ((9 x 8) + (8 x 7) + (9 x 7)) x 1 cm²
Lp = 2 x (72 + 56 + 63) x 1 cm²
Lp = 2 x 191 x 1 cm²
Lp = 382 cm²
Didapatkan luas permukaan balok itu adalah 382 cm².
Dapatkan berita terbaru! Ikuti kami di Google News dan dapatkan kabar terupdate langsung di genggaman.




