
Apa itu kongruen dan kesebangunan?
Kongruen dan kesebangunan merupakan salah satu ilmu geometri, yang di dalamnya juga termasuk kesebangunan dan kongruen bangun datar trapesium dan segitiga. Berikut adalah pembahasan lengkap mengenai kongruen dan kesebangunan dalam matematika.
Pengertian Kesebangunan Bangun Datar
Apa yang dimaksud dengan sebangun?
Kesebangunan merupakan kondisi ketika dua bangun datar memiliki sudut-sudut yang sama besarnya. Selain sudut, panjang sisi sudutnya juga bersesuai dengan perbandingan yang sama. Itu artinya, kesebangunan adalah kondisi ketika dua buah bangun memiliki sudut dan panjang sisi yang sama.
Dalam penulisannya, kesebangunan umumnya dilambangkan dengan simbol notasi ≈. Perhatikan contoh gambar di bawah ini untuk lebih jelasnya.
Dua Bangun Datar yang Sebangun
Kedua bangun tersebut adalah dua bangun yang sebangun dengan beberapa sifat yang sama. Syarat dua bangun datar dikatakan kongruen adalah sebagai berikut.
1. Perbandingan Sisi Sama
Sisi yang bersesuaian memiliki perbandingan yang sama, berikut penjelasannya:
- AD dan EH, memiliki perbandingan AD : EH = 8 : 4
- AB dan EF, memiliki perbandingan AB : EF = 12 : 6
- BC dan FG, memiliki perbandingan BC : FG = 8 : 4
- CD dan GH, memiliki perbandingan CD : GH = 12 : 6
Sehingga dapat disimpulkan bahwa AD/EH = AB/EF = BC/FG= CD/GH menurut uraian di atas.
2. Sudut Sama Besar
∠A = ∠E; ∠B = ∠F; ∠C = ∠G; ∠D = ∠H
Jika berbicara bangun datar, selain memiliki perbandingan panjang yang sama, supaya dapat dikatakan sebangun, dua bangun datar tersebut harus memenuhi dua syarat berikut:
- Sudut-sudut yang bersesuaian sama besar
- Sisi-sisi yang bersesuaian memiliki perbandingan yang sama
Permudah caramu mencari jawaban dengan membuka artikel rumus bangun datar lengkap dengan aplikasi kalkulator yang tersedia.
Pengertian Kongruen
Apa yang dimaksud kongruen? Kekongruenan adalah ketika dua buah bangun datar memiliki bentuk dan ukuran yang sama. Kekongruenan dalam matematika dilambangkan dengan pemakaian simbol notasi ≅. Perhatikan contoh gambar di bawah ini untuk lebih jelasnya.
Dua Bangun Datar yang Kongruen
Gambar bangun segi banyak di atas merupakan kongruen.
Kedua bangun di atas adalah bangun yang kongruen karena panjang KL = PQ, panjang LM = QR, panjang MN = RS, dan panjang NK = SP. Oleh sebab itu, bangun KLMN kongruen dengan bangun PQRS karena memiliki bentuk dan ukuran yang sama.
Dua Segitiga yang Kongruen
Secara geometris, dua segitiga dikatakan kongruen ketika dua buah bangun segitiga dapat saling menutupi dengan tepat. Sifat kedua bangun segitiga kongruen tersebut antara lain:
- Sudut yang bersesuaian sama besar.
- Pasangan sisi yang bersesuaian sama panjang.
Dua segitiga bisa disebut sebagai kongruen manakala bisa memenuhi syarat berikut:
1. Tiga Sisi Sama Besar
Menurut gambar segitiga ABC serta segitiga PQR, diketahui keduanya memiliki panjang AB = PQ, panjang AC = PR, dan panjang BC = QR. Pasangan sisi sisi yang bersesuaian sama panjang.
2. Sudut dan Dua Sisi Sama Besar
Berdasar dari gambar bangun segitiga ABC dan segitiga PQR, dimengerti bahwa kedua bangun memiliki sisi AB = PQ, ∠B = ∠Q, dan sisi BC = QR.
3. Sisi dan Dua Sudut Sama Besar
Dilihat dari gambar bangun segitiga ABC dan segitiga PQR, dimengerti jika, ∠A = ∠P, sisi AC = PR, dan ∠Q = ∠R.
Dua bangun yang sama persis disebut sebagai kongruen. Dalam konteks bangun datar, dua buah bangun datar bisa disebut kongruen apabila memenuhi dua syarat, berikut:
- Sudut-sudut yang bersesuaian sama besar
- Sisi-sisi yang bersesuaian sama panjang
Tertarik belajar lebih jauh tentang segitiga? Buka artikel rumus keliling dan luas segitiga lengkap dengan aplikasi kalkulator yang akan sangat membantumu.
Perbedaan Kesebangunan dan Kekongruenan
Apa perbedaan antara kesebangunan dan kekongruenan? Hal dasar yang membedakan kongruen dan sebangun adalah:
- Bangun dikatakan kongruen jika sisi-sisi yang bersesuaian sama panjang.
- Bangun dikatakan sebangun apabila perbandingan sisi-sisi yang bersesuaian sama besar.
Sehingga dapat disimpulkan bahwa, seluruh bangun yang kongruen sudah pasti sebangun juga. Namun, dua bangun yang sebangun belum tentu kongruen.
Contoh Soal dan Pembahasan
Berikut akan kami berikan contoh soal sekaligus pembahasan mengenai kongruen dan kesebangunan. Perhatikan baik-baik ya.
Soal 1. Soal Cerita Matematika
Tinggi badan Dirga adalah 150 cm. Dirga berdiri pada jarak 10 meter dari sebuah tembok di dekatnya. Ujung bayangan Dirga berimpitan dengan ujung bayangan gedung. Apabila bayangan Dirga sepanjang 4 meter, berapakah tinggi gedung di dekat Dirga?
Jawab:
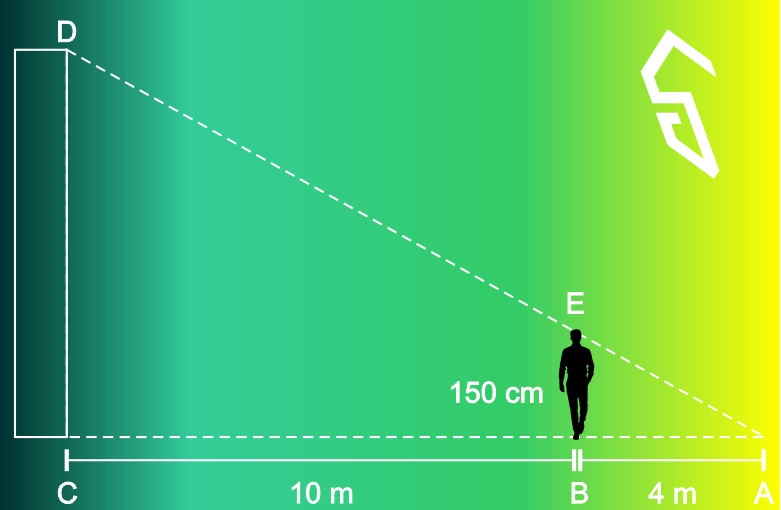
Lihat gambar ilustrasi di atas. Tergambar jelas bahwa Dirga, tembok, dan bayangan membentuk sebuah bangun segitiga ABE dan segitiga ACD. Mengambil prinsip kesebangunan, EB/DC = AB/AC sehingga:
1,5 / DC = 4 / 14
DC = (1,5 x 14) / 4
DC = 5,25
Jadi tinggi tembok di dekat dirga adalah 5,25 meter.
Soal 2. Soal Bangun Datar
Perhatikan gambar bangun datar berikut ini:
Dilihat dari gambar bangun persegi panjang ABCD dan PQRS, kedua bangun datar tersebut sebangun. Sehingga hitunglah:
a. Berapa panjang sisi PS pada persegi panjang PQRS?
b. Berapa luas dan keliling persegi panjang PQRS?
Jawab:
a. Perbandingan sisi AB dan AD bersesuaian dengan sisi PQ dan PS, sehingga berlaku:
PQ / PS = AB / AD
4 / PS = 20 / 8
PS = (4 x 8) / 20
PS = 32 / 20
PS = 1,6
Maka ditemukan panjang sisi PQ yaitu 1,6 cm.
b. Mencari luas serta keliling persegi panjang PQRS:
Seperti yang sudah dijelaskan pada artikel rumus luas persegi panjang, kamu bisa mendapatkan nilai luas persegi panjang tersebut dengan cara sebagai berikut.
L = PQ x PS
L = 4 x 1,6 x 1 cm²
L = 6,4 cm²
Sedangkan untuk keliling persegi panjang, kamu bisa menggunakan cara berikut.
K = 2 x (PQ + PS)
K = 2 x (4 + 1,6) x 1 cm
K = 11,2 cm
Soal 3. Soal UN Matematika SMP 2016
“Lebar Sungai”
Fani ingin mengetahui lebar sebuah sungai. Dari tempatnya berdiri, Fani melihat sebuah pohon di seberang sungai. Untuk mengetahui lebar sungai tersebut, Fani menancapkan beberapa tongkat agar memudahkan penghitungan. Tongkat tersebut berada di titik A, B, C, dan D seperti pada gambar berikut.

Fani ingin mengukur lebar sungai dari tongkat di titik D sampai pohon. Berapa lebar sungai tersebut?
A. 16 meter
B. 15 meter
C. 12 meter
D. 11 meter
Pembahasan:
Untuk menjawab pertanyaan tersebut, mari sejenak lihat gambar berikut ini.
Lebar sungai tersebut dapat dihitung dengan memanfaatkan prinsip kesebangunan segitiga.
Lebar sungai = DP
DP / AP = DC / AB
DP / (4 + DP) = 6 / 8
8DP = 6 x (4 + DP)
8DP = 24 + 6DP
8DP – 6DP = 24
2DP = 24
DP = 24 / 2
DP = 12
Jadi, lebar sungai yang ada di hadapan Fani adalah 12 meter.
Jawaban: C
Soal 4. Soal UN SMP/MTs Tahun 2010
Perhatikan gambar berikut ini!
P dan Q merupakan titik tengah diagonal BD dan AC. Panjang garis PQ adalah ….
A. 2 cm
B. 3 cm
C. 4 cm
D. 5 cm
Jawab:
Rumus cepat untuk memperoleh panjang garis PQ adalah dengan cara:
PQ = 1/2 (DC – AB)
PQ = 1/2(12 – 6)
PQ = 1/2 x 6
PQ = 3
Jadi, garis PQ memiliki panjang 3 cm.
Soal 5. Kongruen dan Kesebangunan
Pasangan bangun datar berikut yang pasti sebangun adalah ….
a. Dua segitiga sama kaki
b. Dua jajaran genjang
c. Dua belah ketupat
d. Dua segitiga sama sisi
Untuk menjawab pertanyaan tersebut mari ingat kembali syarat dua bangun datar disebut sebangun.
- Perbandingan panjang sisi yang bersesuaian sama
- Sudut yang bersesuaian sama besar
Pada segitiga sama sisi, ketiga sudutnya sama besar yaitu 60 derajat, sehingga jika ditemukan dua segitiga sama sisi maka sudut yang bersesuaian pasti sama besar.
Selain itu, sisi-sisi pada segitiga sama sisi panjangnya selalu sama. Sehingga, bila diberikan dua segitiga sama sisi maka pasti perbandingan panjang sisi yang bersesuaian sama.
Jadi, apabila terdapat dua segitiga sama sisi pasti bangun datar tersebut sebangun. Sehingga, jawaban yang benar adalah D.
Itulah yang dapat kami sampaikan terkait kongruen dan kesebangunan. Semoga ulasan ini dapat kamu jadikan sebagai bahan belajar kalian ya.
Dapatkan berita terbaru! Ikuti kami di Google News dan dapatkan kabar terupdate langsung di genggaman.
